This Saturday two of the best teams in the world, Juventus FC and Real Madrid FC are playing the final of the best club competition in the world, the UEFA Champions League in Cardiff, UK.
This motivated me to write an online blog for Chalkdust magazine. The content of the article is the mathematics and the science behind, from my point of view, the most spectacular goal I have ever seen in my life, the famous free-kick taken by Roberto Carlos in 1997. The very first time I watched it, I was a kid and I was so impressed by this goal that I could not find an explanation to it: how it was possible that the ball bent drastically and landed in the goal when it seemed that it was heading in a totally different direction. As a kid, you always try to do what your heroes do (in my case, Roberto Carlos was and still is one of my favourites football players), and I was not an exception: I tried to kick my football trying to replicate the “weird” effect seen in Roberto Carlos’ free kick. I never succeeded (just on a few occasions, but not quite good).

I grow up and my interest in science during my adolescence increased, which motivated me to begin to read scientific magazines. I remember that time when I was reading one of my very first magazines, I surprisingly found an article explaining the physics behind Roberto Carlos’ goal: my favourite sport and science combined in an excellent read. Unfortunately, the concepts involved there was still a bit complex for me in order to completely understand it. But I promised myself: one day, I have to be able to study in detail this goal. And now that I am a Ph.D. student in mathematics and working in fluid mechanics, finally decided to do it. It was not easy though, but quite funny. A lot of information regarding this topic can be found in many scientific journals. I read some of them and managed to write my very own version of an article explaining the science and mathematics about free kicks (more specifically, Roberto Carlos’ one).

You can completely read it here. Here in this blog, I will show some stuff that could not be included in the original article.
Initial conditions
In the article, we mention that in order to solve our system of differential equations, we need six initial conditions. Three of them are the elements of the vector position. The other three are the components of the vector velocity, which have to be determined using the diagrams below:

The values of the angles shown in the diagram above were determined by the scientists. These values are used to calculate the components of the initial vector velocity:

Using a bit of trigonometry and geometry, relations for the initial vector velocity are found:
MATLAB Code
For any person interested in simulating their own football free kick, I provide the code I used to obtain the curves and plots shown in the original Chalkdust online article. I used the MATLAB software to introduce my equations, as shown below:

You only need to open a new script in MATLAB and write down all the equations. The text in green indicates what the symbols and the equations stand for.

Once that you have finished, just type in the command window the values of the variables required by the function rocarlosfk(t,y,d,p,m,w0):
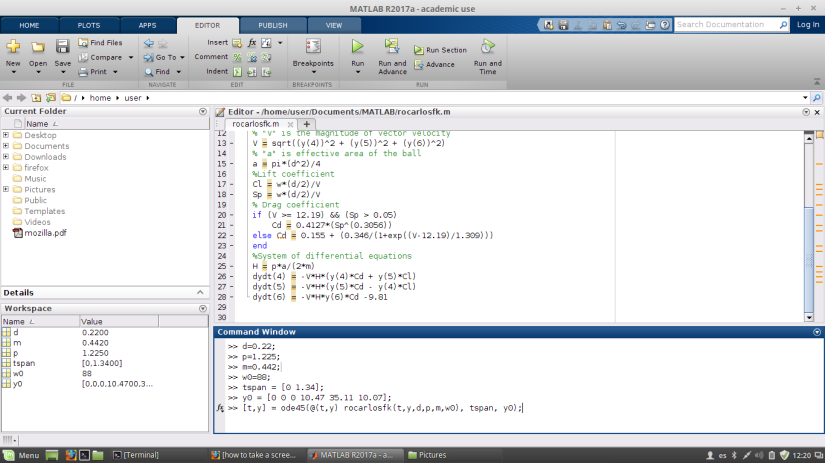
You need to specify the interval of time you wish to calculate the solutions of the system of ODE’s. In this case, this is introduced in tspan. The initial value is at time t=0 and the final time is 1.34 s.
The initial conditions are introduced as y0 in vector form (see the picture). The first three elements are the components of the vector position and the last three are the components of the initial vector velocity. Finally, you call the solver ode 45 as follows:
[t,y] = ode45(@(t,y) rocarlosfk(t,y,d,p,m,w0), tspan, y0)
To see the solutions of the system, you plot the results using the plot3 function. After you run the code that calculates the solution of the equation, you simply have to type the following command:
plot3(y(:,1),y(:,2),y(:,3),’-o’)
That command will show a three dimension plot, where y(:,1) means coordinate x, y(:,2) is coordinate y, and y(:,3) is for coordinate z. The ‘-o’ is simply to plot the results as a dotted line.
The code shown above is for the simulation of Roberto Carlos’ free kick. But you can simulate your own football free kicks using different conditions. Try changing the angles, the density of the air, the magnitude of the vector velocity. The only fundamental thing is that you have to satisfy the conditions mentioned in the online article and the equations shown here for the components of vector velocity. The lines of the MATLAB code I used to obtain the free-kick curves can be found here rocarlosfk. Check it out.
If you want to know more about maths in football, see also these blogs written by me:
- “Bend it like Newton: curves in football“.
- “The maths behind a chip goal” (ShortList magazine article and Chalkdust online blog).



Can you tell me how to ply the graph and what variables to use for the graph? Thanks
Best Regards
LikeLike
After you run the code that calculates the solution of the equation, you simply have to type the following command:
plot3(y(:,1),y(:,2),y(:3),’-o’)
That command will show a three dimension plot, where y(:1) means coordinate x, y(:2) is coordinate y, and y(:3) is for coordinate z. The ‘-o’ is simply to plot the results as a dotted line.
LikeLike
Hello!
Thank you for this. However, I believe there is a mistake incurred in calculating vx, vy and vz. I am not getting 10.47 as a value for vx no matter what I do, I am getting 3.18. Am I doing something wrong?
So I understand that alpha =16 degrees and gamma = 5 degrees
Convert these to radians, then get the value of theta and phi.
After this, substitute in the equations above and you will get (3.18, 36.35 and 10.47).
Thank you.
LikeLike
Hi.
Thanks for your observation. And I just noticed that you are right. I made a mistake in the Chalkdust article and I somehow wrote incorrect values of the initial velocity (I probably wrote the values of another case). The ones that you reported (3.18,36.35,10.47) are the correct ones. The figures will slightly change but you can still reproduce the bending effect. Apologies for the confusion.
Hugo
LikeLiked by 1 person
Hello sir!
As an ardent football fan and mathematics lover, I have truly been fascinated by all your articles here and on the ChalkDust blog. I have understood the mathematics behind Roberto Carlos’s free-kick and was keen to model it myself on MATLAB Online using the code you provided. However, after I copied this exact code into MATLAB and ran all the instructions as shown in this article, I did not get the model of the freekick. Instead, I got a parabola. I am extremely confused about where I have gone wrong. I would be extremely grateful if you could help me out with the same.
Thank you so much!
LikeLike
Hello Kushal,
sorry for the late reply.
I am very glad to hear that you have enjoyed reading my articles. I am also happy to help you with your question.
What parameter models (d,p,m,w0, tspan, y0) are you using ? I introduced these ones into the code: d = 0.22 m, p = 1.225 kg/m^3, m = 0.442 kg, w0 = 88 rad/s, tspan (in seconds) has to be specified in vector form, the initial value is at time t=0 and the final time is 1.34 s, thus tspan= [0 1.34], and y0 is the vector of initial conditions for the position and the velocity and has to be also specified in vector form, y0 = [0 0 0 3.18 36.39 10.47]. Once that you introduced these parameters into the code. You might not get a plot similar to the one I reported in the Chalkdust article (I realised I did a mistake in calculating the angles), but you should be able to get the parabola with the bending effect. Let me know if that works
LikeLike